

(2x – 3) (2x + 6) = 0 Changing from Intercept Form to Standard FormĪ quadratic equation can be transformed from its intercept form to its standard form by multiplying and simplifying (x – p) (x – q): We’ll now factorize the quadratic equation to solve it. To find p and q, we simply utilize any of the quadratic equation solving methods.įor the quadratic equation 4x 2 + 6x – 18 = 0. The x-intercepts of the quadratic function f(x) = ax² + bx + c = 0 are (p, 0) and (q, 0), respectively, therefore p and q are the roots of the quadratic equation. Changing a Quadratic Equation from Standard to Intercept FormĪ (x – p)(x – q) = 0 is used to transform the standard form of a quadratic equation to the vertex form. Therefore by substituting (x – h) 2 = (x – h) (x – h),ģx 2 – 4x + 13 = 0, which is in Standard Form. Rewrite quadratic function in standard form: 2 (x 2 – 2x + 1) + 1 = 0 Changing from Vertex Form to Standard Formīy evaluating and simplifying (x – h) 2 = (x – h) (x – h), a quadratic equation can be converted from its vertex form to its standard form: Now we can rewrite Vertex Form into Standard Form as:į(x) = a(x – (-b) 2a )² + 4ac – b² 4a = 0įor Example, For a Standard Quadratic Function f(x) = 4x² + 3x + 10 = 0 Now comparing constants on both sides we get, Therefore, equating a Standard Quadratic function and Vertex Quadratic functionĪx 2 + bx + c = ax 2 – 2ah x + (ah 2 + k)Ĭomparing the coefficients of x on both sides, Where, (h,k) is the vertex of the quadratic function f(x). The standard form of a quadratic function is also referred to as the general form of a quadratic function.Įxamples of Standard Form of Quadratic Equation:Ĭhanging a Quadratic Equation from Standard Form to Vertex Form The leading coefficient is always a non-zero real number, and it is denoted by ‘a.’ Otherwise, the function will not be quadratic since the greatest degree of 2 will not exist. Here a, b, and c are the constant coefficients and x is the unknown variable with the highest degree of 2, a is never equal to zero, making f(x) a quadratic function.
Vertex of quadratic function how to#
This is how to write the quadratic function in standard form: How to write a quadratic function in standard form?

Quadratic Functions can be represented in 3 forms:

Quadratic Functions are so named because Quad stands for ‘four’ (squared), and a quadratic function’s greatest degree should be 2. Thus, the vertex of the graph is $latex (-3, -11)$.Quadratic Functions are defined as second-degree polynomial equation, which means it has at least one term with a power of two. For example, we have already seen its standard form: Quadratic equations can be presented in different ways.
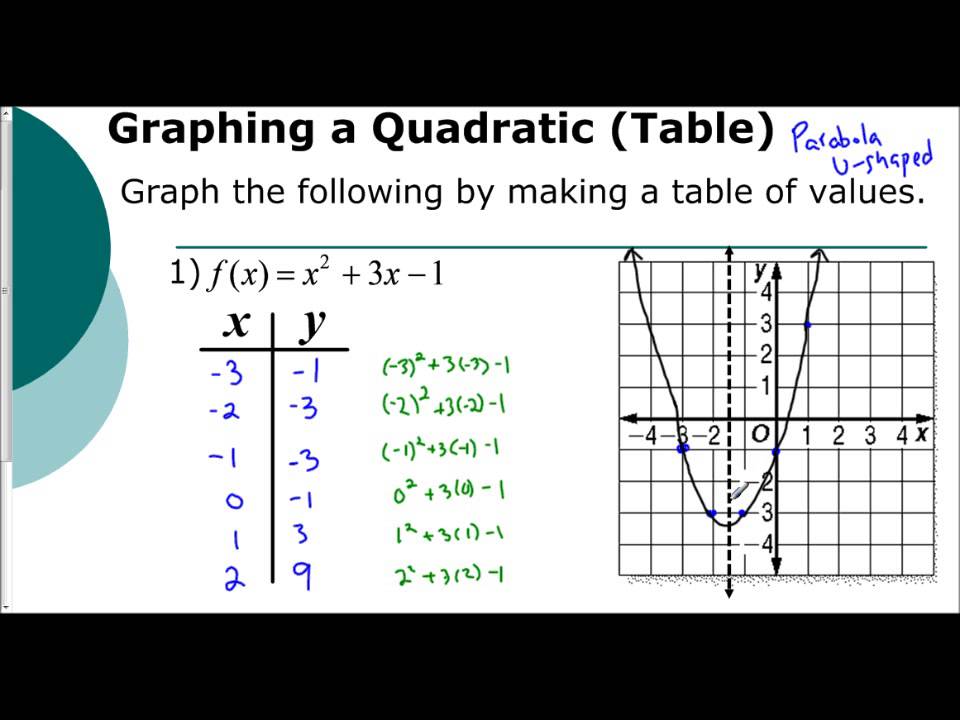
The vertex form of a quadratic function allows us to find the vertex of the graph easily. Graphs of quadratic functions in vertex form When the parabola has two x-intercepts, the vertex always lies between these intercepts due to the symmetry of the graph. The number of intercepts depends on the location of the graph of the quadratic function. It is possible to have zero x-intercepts, one x-intercept, and two x-intercepts. The x-intercepts represent the zeros or the roots of the quadratic function, that is, the values of x when we have $latex y = 0$. The x-intercepts are the points where the parabola crosses the x-axis. If there were more y-intercepts, the graph would not represent a function. For all graphs of quadratic functions, there is a single y-intercept. The y-intercept is the point where the parabola crosses the y-axis. This vertical line passes through the vertex. Axis of symmetryĪll parabolas are symmetric with respect to a vertical line called the axis of symmetry. If the parabola opens upwards, the vertex represents the lowest point and if the parabola opens downwards, the vertex represents the highest point. The vertex is the extreme point on the graph of a quadratic function, that is, it is the highest point or the lowest point. These parameters are the vertex, the axis of symmetry, the y-intercept, and the x-intercepts. Parabolas have different parameters that determine their shape and their location in the Cartesian plane.


 0 kommentar(er)
0 kommentar(er)
